高低压开关柜柜体的一些安装规范

13 11
美国大选:几何学与选区的不公正划分
方格1按照每个党派的选票分配比例划分选区。同样是这个方格,经过“打包”和“拆分■■◆■★■”之后能产生完全不同的两种选举结果■■★■■,如方格2和方格3——蓝色党派在方格2中赢得了全部的选区,在方格3中只赢得了4/10的选区★■■■。在这个极端例子中◆◆■★,选举结果有利于蓝色党派★◆。我们使用马尔可夫链蒙特卡罗统计分析方法,可以发现在所有可能的划分结果中,橙色党派更倾向于赢得2~3个席位,而不是按照选票分配的比例计算出的4个席位。
2016年,我同几位朋友成立了专门工作组来研究几何与计算在重新划分美国选区中的应用。之后,我们小组将工作范围扩大到培训和咨询领域。共有1200多人参加了我们在全国各地举办的培训班■◆■◆,其中许多人积极参与了选区重新划分项目。我们认为■★★◆◆■,是时候将数学计算纳入研究了。选区不公正划分问题涉及非常丰富的数学知识——足够单独成为一个数学研究分支,而现有的数学计算能力仅仅能勉强应对重新划分问题的计算规模和复杂性。我们希望在下一次美国人口普查需重新划分选区之前建立好实践工具和理论框架★■◆◆■★。
美国全国范围内的法律事件和头条新闻中时常出现不公正划分选区(Gerrymander)的案例■■■★◆■。比如美国联邦最高法院曾审理过一些关于选区合宪性的案件,据称这些案件中的选区划分为威斯康星州的共和党和马里兰州的创造了巨大优势,但法院回避了对这两个地区的直接裁决。来自北卡罗来纳州的另一个党派分歧案件在2018年8月下级法院的强烈呼声中曲折推进◆★。但到目前为止◆★,还不可能出现一个可供法官判断某选区是否被不公正划分的法律标准★★★◆◆◆。正如美国联邦最高法院前官安东尼·肯尼迪(Anthony Kennedy)在2004年的一宗案件中所指出的那样,问题的一部分在于★◆★■★,无论是下级法院还是上级法院,都尚未确定一个“可行的标准”来判断选区是否被不公正地划分★★■◆■。这就是美国各地有越来越多的数学家认为我们可以提供帮助的地方。
在一个赋予被选举者巨大权力的国家■■,总是会发生控制选举进程的小规模冲突事件■■。在众议院这样的体制中,每一个选区的获胜者都能获得该选区的全部选票■◆★■◆,选区的划分就成为一个天然的战场。美国历史上充满了令人震惊的选区划分计划,从利用在职总统的权威拉拢选区■◆,到以三种不同的方式划分同一个选区,再到压制黑人选民的政治权利★◆■★■。这些操作变换着形式,换汤不换药,在今天仍在继续,在大数据时代,它们变得更加复杂。现在比以往任何时候都更难以确定选区再分配的权力是否被滥用。人们通常认为选区 的不公正划分有两个特点——奇怪的选区形状和不成比例的选举结果——但这两个特点都不足以作为选区不公正划分的判定标准★■■。那么,我们该如何判断天平是否倾斜向不公正的一方■■?

以上内容节选自《21世纪的数学:探索人类认知的边界》◆■,由机械工业出版社出版。数学与我们的生活息息相关,同时伴随着人类文明的发展而不断进化◆★■◆。21世纪的数学已经演变成一种抽象的艺术形式,具有其独特的内在审美价值◆★★◆。本书精选了全球十几位杰出科学家的研究成果,从纯数学理论的研究前沿◆■,到数学与生命◆■◆、物理及人类文化的关系,再到数学所存在的固有局限性★◆,展示了现当代的伟大数学成就。
1787 年,麦迪逊在《联邦党人文集》中写道:“民主的自然极限是距离中心点的一段距离◆◆■,这段距离刚好满足最偏远公民为履行公共职能经常参加集会的需求。”换句话说,选区应该是可连通的■★★■◆。1901年,一项联邦分配法案标志着美国法律首次出现了一个模糊的要求,即划分的选区应该由■◆★◆“紧凑的领土”组成。◆★■★“紧凑■★◆■” 一词随后在选区划分的相关法律中广泛出现,但几乎没有确切的定义。进行州长选举的37个州都有对选区形状的规定,几乎每一种情况都是依靠肉眼判断选区是否被公正地划分。问题是★◆,一个地区的轮廓所给出的信息是非常片面和具有误导性的。一方面◆◆■■★,扭曲的形状背后可能有良性的原因◆◆◆■★。这样的边界可能是自然形成的,也可能是出于团结社区的目的划分的,但这些因素通常作为不公正的选区划分结果的替罪羊。另一方面★◆★■◆,相对规则且对称的选区划分并没有具有说服力的质量证明■★。
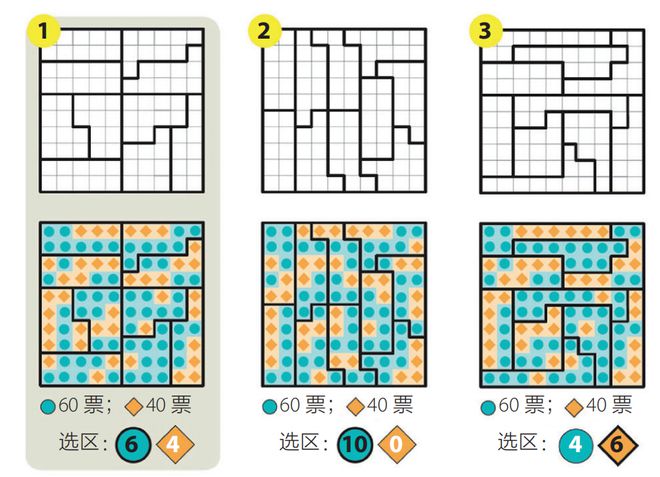
不公正划分选区依赖于精心绘制的线条,通过将对手政党的选民集中到少数几个人数过高的选区(“打包”),或稀释对手政党的选民,将他们分散到不同选区◆◆◆★,使他们不能选出偏好的候选人(“拆分”)◆◆■★★,或者使用两种方案的组合。
如果形状不是不公正划分选区的可靠指标,那么对比选举结果在多大程度上与选民的投票模式相匹配是否有效呢◆★★?显然◆◆◆■■,不平衡的结果提供了不公正划分选区的初步证据。让我们看看全州范围内的角逐,这样我们就可以把无争议席位和其他混杂变量放在一边。以肯尼斯·蔡斯为例,他是2006年的参议院竞选中泰德·肯尼迪的竞争对手,在全州范围内赢得了超过30%的选票。从比例上讲,你会期望蔡斯在九个国会选区中的近三个选区击败肯尼迪。但实际上并非如此。事实证明,在数学上不可能找出一个由城镇群或者地区构成的单独选区倾向于蔡斯。他的选民根本不够集中。相反,大部分选区支持蔡斯的人数都接近州平均水平,所以说支持蔡斯的选区还不够。任何有投票权的少数群体在选票的分配上都需要具有一定程度的多样性,以为我们的分配系统提供一个理论上的证据来确保其代表性★★■■。对蔡斯—肯尼迪案的分析甚至没有考虑空间因素,例如以肉眼判断的标准◆★■◆■■,每个区域应该是连通的。人们可能会理所当然地想知道,在令人惊讶的众多可能的选区划分方案面前★★,我们如何对其公正性与合理性做出解释★■■★◆◆。
